In this section we explore in depth the concepts behind #1 by introducing the one-sided limit. We begin with formal definitions that are very similar to the definition of the limit given in Section 1.2, but the notation is slightly different and "\(x\neq c\)'' is replaced with either "\(xc\).''
Definition 2: One Sided Limits
Left-Hand Limit
Let \(I\) be an open interval containing \(c\), and let \(f\) be a function defined on \(I\), except possibly at \(c\). The limit of \(f(x)\), as \(x\) approaches \(c\) from the left, is \(L\), or, the left--hand limit of \(f\) at \(c\) is \(L\), denoted by
means that given any \(\epsilon > 0\), there exists \(\delta > 0\) such that for all \(x< c\), if \(|x - c| < \delta\), then \(|f(x) - L| < \epsilon\).
Right-Hand Limit
Let \(I\) be an open interval containing \(c\), and let \(f\) be a function defined on \(I\), except possibly at \(c\). The limit of \(f(x)\), as \(x\) approaches \(c\) from the right, is \(L\), or, the right--hand limit of \(f\) at \(c\) is \(L\), denoted by
means that given any \(\epsilon > 0\), there exists \(\delta > 0\) such that for all \(x> c\), if \(|x - c| < \delta\), then \(|f(x) - L| < \epsilon\).
We practice evaluating left and right-hand limits through a series of examples.
Example 17: Evaluating one sided limits
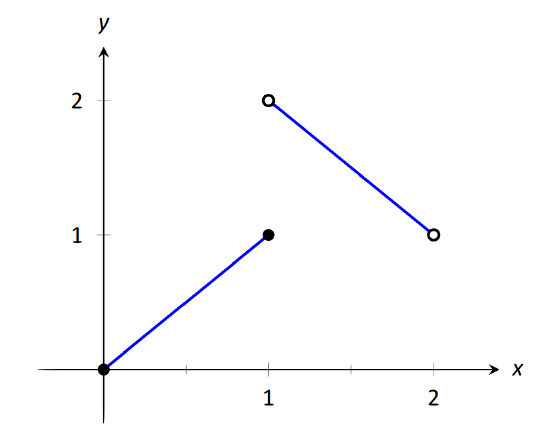
Let \( f(x) = \left\ x & 0\leq x\leq 1 \\ 3-x & 1,\right.\) as shown in Figure 1.21. Find each of the following:

\(\text\): A graph of \(f\) in Example 17.
Solution
For these problems, the visual aid of the graph is likely more effective in evaluating the limits than using \(f\) itself. Therefore we will refer often to the graph.
Note how the left and right-hand limits were different at \(x=1\). This, of course, causes the limit to not exist. The following theorem states what is fairly intuitive: the limit exists precisely when the left and right-hand limits are equal.
Theorem 7: Limits and One Sided Limits
Let \(f\) be a function defined on an open interval \(I\) containing \(c\). Then \[\lim\limits_f(x) = L\]if, and only if, \[\lim\limits_f(x) = L \quad \text \quad \lim\limits_f(x) = L.\]
The phrase "if, and only if'' means the two statements are equivalent: they are either both true or both false. If the limit equals \(L\), then the left and right hand limits both equal \(L\). If the limit is not equal to \(L\), then at least one of the left and right-hand limits is not equal to \(L\) (it may not even exist).
One thing to consider in Examples 17 - 20 is that the value of the function may/may not be equal to the value(s) of its left/right-hand limits, even when these limits agree.
Example 18: Evaluating limits of a piecewise-defined function
Let \(f(x) = \left\ 2-x & 0,\right.\) as shown in Figure 1.22. Evaluate the following.
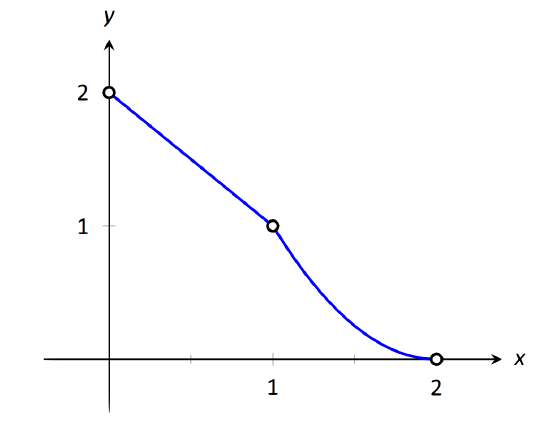
\(\text\): A graph of \(f\) from Example 18.
Solution
Again we will evaluate each using both the definition of \(f\) and its graph.
Example 19: Evaluating limits of a piecewise-defined function
Let \(f(x) = \left\ (x-1)^2 & 0\leq x\leq 2, x\neq 1\\ 1 & x=1\end,\right.\) as shown in Figure 1.23. Evaluate the following.
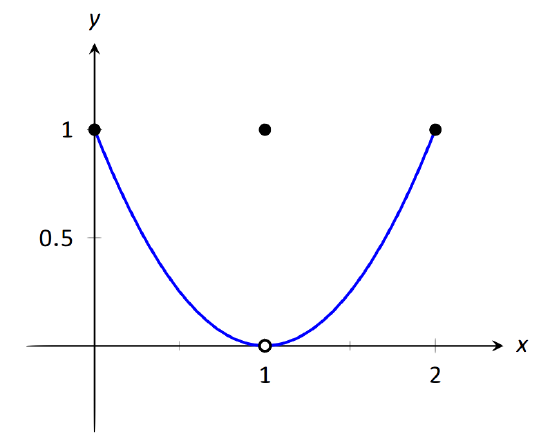
\(\text\): Graphing \(f\) in Example 19.
It is clear by looking at the graph that both the left and right-hand limits of \(f\), as \(x\) approaches 1, is 0. Thus it is also clear that the limit is 0; i.e., \( \lim\limits_ f(x) = 0\). It is also clearly stated that \(f(1) = 1\).
Example 20: Evaluating limits of a piecewise-defined function
Let \(f(x) = \left\ x^2 & 0\leq x\leq 1 \\ 2-x & 1
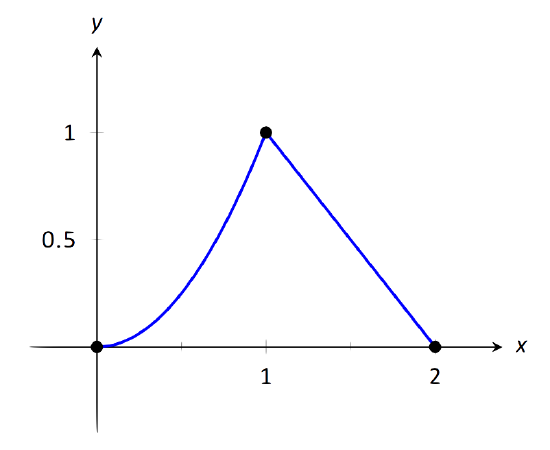
\(\text\): Graphing \(f\) in Example 20.
Solution
It is clear from the definition of the function and its graph that all of the following are equal:
\[\lim\limits_ f(x) = \lim\limits_ f(x) =\lim\limits_ f(x) =f(1) = 1.\]
In Examples 17 - 20 we were asked to find both \( \lim\limits_f(x)\) and \(f(1)\). Consider the following table:
Only in Example 20 do both the function and the limit exist and agree. This seems "nice;'' in fact, it seems "normal.'' This is in fact an important situation which we explore in the next section, entitled "Continuity.'' In short, a continuous function is one in which when a function approaches a value as \(x\rightarrow c\) (i.e., when \( \lim\limits_ f(x) = L\)), it actually attains that value at \(c\). Such functions behave nicely as they are very predictable.
2.4: One-Sided Limits is shared under a CC BY-NC-SA license and was authored, remixed, and/or curated by LibreTexts.